2010年11月28日日曜日
1-1-2 カード_10
すなわち、個々の事項(粒子)を集めて(①再帰・合わせ鏡)、それを並べる(②創発・剣)ようなものであった。コーネル方式や三本線のように、内容を1つにまとめる(③相転移・玉、一言化)、というような部分は共通認識ではないようであった。
実際の授業では、このように内容を理解しながら、それと並行してきれいに揃えながら、きれいにまとめてゆく、という2つ以上の作業を同時に行うのは、物凄くストレスがたまると思われ、これが出来るものが東大生、という印象を受けた。
きれいに書く、というのは、個々の事項をなるべくくっきりと明確に分けながら記述してゆく、という効果があるように思われ、カードもまた同じ効果があると考えられた。
1-1-2 カード_08
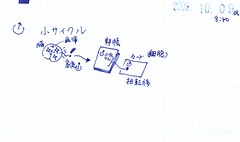
頭の中のイメージが野帳へ描き付けられるまでの小サイクル
①頭の中のもやもや(粒が飛び交う、波がめらめらしている状態。これは再帰・合わせ鏡の間の共鳴)
②複数のもやもやが、頭の中で1つのかたまりのように積み重なっていく(創発)
③これが1つの言葉・イメージになり、野帳に描き付けられる(相転移)
野帳からカードが生まれるまでの小サイクル
①野帳の中にメモ・記述がたまる(再帰)
②ざっと見て、カード化する項目を1つ選ぶ(順番を決める。創発)
③1枚のカードが産まれる(相転移)
1-1-2 カード_07
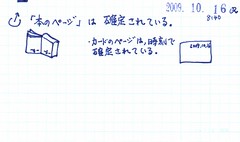
日付によりナンバリングされたカード、これは、収束感(左脳的)があり、一方、感情的な感覚(右脳的)にも繋がっています。この文章を打ち込んでいる時点で、このカードの日付と時間を見ると・・・「1年と1ヶ月前の秋、金曜日の朝に描いたカード」。
1-1-2 カード_06
実際には、結構頑張って、1年でやっと一杯になる程度でした。というのは、①野帳に発想を描き付ける、これは文章にすると長くなるかもしれない事項を、一瞬のイメージで一言化・図化しているので、1年で野帳何十冊、という消費はありえない。一方、野帳からカードへの転記は、内容のフィルタリングや転記作業量の制限がかかってて、平均すると多い日でも1日で5牧程度です。このことから、日常では容量やカードの大きさを気にする必要はないことが解りました。
2010年11月13日土曜日
GTDカード(試行中)
TODOは①仕事中や②ふとした時に発生する。Aをやっているときに、Aに関連したBもやらなければ、とか、隣の部屋に行ってCもやらなければ、とか、やってる途中にどんどん増える。逆に、机の上で「う~ん」とうなっても、大して思い出せない(その一方でシミュレーションすることで、ものすごく頭と精神が疲れる、実際には何もしていないのに・・・)。
だから、TODOを、思い出して書く必要はない。頭の負担を下げるためのTODO管理やGTDリストのはずだから。PoICでは野帳でコーヒータイムや風呂中の発想を捉えるように、仕事上のTODOを①仕事中や②ふと発生したときに捉える。
最近は、TODOを思いついたら、野帳に貼ってあるポストイットに書き付けている(1分後には忘れるので)。そして、すぐ終わるものはそのまま行う。すぐ終わらないものは、GTDカードに貼る(ポストイットだと、転記しなくていい)。
GTDカードは、今使ってるのは、真ん中に円があり、右に8つの小さい円がある。
真ん中の円には薄く白くて四角いスペースがあって、ポストイット(半分に切ったサイズ)を貼れるようにしている。ポストイットに描いてあることは、描いた時点では「あ、これをしなくては」という事項で、これはTODOだけど、作業手順ではなく、その内容は後から見ると結果的に仕事の小単位のテーマ(目標・主題)になっている。
右の小さい丸は8つあって、そこに次やることを、イメージで思いついたのを1つ(か2つか3つ)だけ描く。この項目描き出しに際し手順はどうでもよく、次にやることを描く。わっと気分的に一番に頭に浮かぶこと。それは、①次にやること、または②内容的(実質的)には目的の8割を占める、2割の項目である。気分から発したその項目だけを、やればいい(やることに、間違いはない!)。そしてそれをやっていたら、すぐに次に(他に)やること(「これもやらないと」)が、自ずと思いつくから、やっている途中に小さい丸に描き足す。こうして、具体的なActionのリストは、作業実施中に、自然に現われてくる。
仕事の「段取り・手順・最終型」を{考えて・シミュレーションしながら}、「う~ん」とうなりながら、最後まで描く、ということはしない。頭の負担を減らすためのカードなのに、そこで「う~ん」とうなったら、本末転倒だから。で、右の小丸の手順はやってる時に次々と自動的に埋まっていく(ので、手順を考える必要もない)。どうせシミュレーションしても有機的に変わって行くし、超整理法でも分類は諦めたように、TODOでもActionの細かい管理(時系列的な順番を決めること)はしない(無意味)。
(※「メタ」で行わなければいけないのではないだろうか。例えば、超整理法では、整理を、整理の「中の世界(!)」の作法である「分類」をせずに(動的に変わっていくから)、整理の「外の世界(つまりメタ・外からの視点)」である、”整理”そのものとは全く関係の無い(!)時系列で管理(というか並べてある)している。ここでTODOの目的・テーマを達するための複数の個々の項目について、これらは実行することや割り込みが入ることで、時間的に変化していく、つまり時間に対して「動的」である。だから変動するから、順番まで決めたアクションリストを作って、その順番にこなしてゆく、という、いわゆる「アクションリスト」は、せっかく一生懸命に作っても、やっている最中に破綻する可能性が(かなりの確率で)高いのでは。だから、時間順は考えずに、次にやることを、ぽつ、ぽつ、と描き出すのみとする。あえて分類・整理・順列化するとしたら、それは「時間軸」ではなく、「空間・場所」とか個々の項目の「質」とか、「まとめて、同時にできるか」とか、時間とは別の、なんらかの軸ではないだろうか)。
むしろ、どんどん増えるTODOを増えるがままに増やしていって、自分の仕事だったら複数の部屋にわかれているので、GTDカードを部屋ごとに分けて、その部屋に移動する毎にそこでできることをこなしていく、というふうに、「”ついで”を自動的に”まとめる”」ことが必要だと思われる。
中心の丸の左側は開けてある。これは、岡田斗司夫のノート術を参考にしている。仕事中のデータやメモ、思いついたことや発展やらが(もしあれば)描いておく(無ければ何も描かなくていい)。思いついたことを覚えておくことによる頭の負担を減らす効果がある(精神的負担をカードに移す)。
右の8つの丸が埋まったら、左にも書き足していけばいい、とは思っているけど、実際はそんなに増えることは{滅多に・ほとんど}無い。
このGTDカードはマインドマップみたいに放射状に書き込めるようにしてある(実際は右側の、上の丸から下に向かって、やる項目を描いていくことが多いけど)。
真ん中の丸は、以前は陰陽☯のマークにしていたけど、今はシンプルにした(、しかし内容的には☯)。
右の小丸の項目が再帰的ルーチンワーク(プログラムのサブルーチン)で、それが上から下に進みながら蓄積していったら(創発)、結果(直近の、または蓄積して遠い未来に別の形での)が得られる(相転移)の流れになるようにしている。
右の丸は、やるたびにチェックしていく。これは、やり終えた後ではなく、やり始めるときにチェックする。その方が物事が前に進む。やり終えた後のチェックは、精神衛生上よくない。
検討中の事項は、
・カード全体の図案とか、
・真ん中の丸の大きさとか、形とか、
・右の小さい丸の数、
・そして進めるごとにするチェックが赤ペンがいいのか蛍光ペンがいいのか、チェックのマークは「v」がいいのか、もっと丸みを帯びた、あるいはちょこっと描き足すことで何らかの絵になるようなもの(だるまの目を埋めるように)が無いか、
・そもそも右の丸は、蓄積していくもの、これは自然界では落ち葉や水滴、地層のようなもので、それを表すシンプルな形が、丸でいいのか、もっといいものはないのか
・右の小丸は、中心のテーマから生じたもの、これは貝の殻のように、中心から放射状に放出してゆくもの、小丸の配置もやや放射状にしてあるけど、それでよいのか、
・一番上の丸は日付に近くて、文字を描いたときに両者が淀んで混じって見えてしまう、
・このGTDカードは
www.flickr.com/photos/36761543@N02/5163347036/
と同じ形をしている、つまり上述のカードの下の平面(xi軸の面)にあたる、だから真ん中の円はz軸(高さ、手前)に向かって伸びてくる螺旋(巻貝、炎)に相当する、そして右側は上から下に(上下方向)、左側は中心から左に(左右方向)伸びていて、これは直交していて複素数のようでもあり、脳や岡田斗司夫のノートの構造(右ページに論理的項目を書き、左ページに右から派生したイメージを描く)にも対応している、ここで
www.flickr.com/photos/36761543@N02/5163347036/
の構造をよりよく現すような、図案や構造は無いだろうか、そして一方ではシンプルに、
(例えば遺伝子のように螺旋で蓄積してゆくデータ、貝、炎、PoICのエントロピーモデル、etc)
・カード全体の5mmの格子(とりあえずエクセルで方眼)は濃いほうがいいのかそれとも薄く、あるいは無い方がいいのか、
・最初にポストイットを貼る位置はマインドマップ的にカードの中心の丸の中心がいいのか、それとも真ん中の丸は陰陽(☯←このマークを90度傾けたもの)だからその再帰が発するところは丸の上側でそこにポストイットを貼ってスタート地点としたほうが良いのか、
・右側の小丸は8個だけれども、これは数が制限されている、マインドマップ的に分岐する余地をもたせてゴッホの渦やフラク的に間が埋まっていく構造にした方がよいのか、そもそも丸ではなくマインドマップのように線(枝)を放射状に広がるように描いておいて、そこに書き込むようにしたほうが良いのか、
真ん中の丸(テーマ)から小丸が派生した、これは人間の体全体と手のひらが似ているように、真ん中の丸と小丸にも有機的なつながりをもたせたイメージをもたせたほうが良いのか
・真ん中の丸と周りの小丸、これは形のある粒だけれども、ゴッホの渦のような、形(輪郭)の無い構造ではどうなのか、霧の中にTODOが自発的に生み出される連鎖的な形が浮かび上がるような、
・・・などなど、どんなのがいいのか、まだ使いながら様子を見ている段階で、全然確定していない、ので、エクセル上で創ったのをわら半紙や裏紙に印刷してはさみで切って大量に用意しておいて、使いながら様子をみているところ。
(職場に余っている青い罫線の方眼紙にも印刷してみた、のもある)。
図案が確定したら、コレクト(またはダイソーの)情報カードに印刷する予定(それとも、今の薄いわら半紙でもいいのだろうか)。
------------
(追記)
ふと、丸の図案を「珪藻」にするのはどうかと思った。小さい丸は、蓄積していくもの。珪藻は水に沈んでゆき、地層の珪藻土になる。
「珪藻」
micro.sakura.ne.jp/mws/mws_j_series_1st.htm
あまり動的なイメージではないけれども、
・・・丸が珪藻だったら、GTDカードが標本の世界みたいで、何かいいかも(^^;
天体、月面
図案みたいなのではなくて、ほんとの写真から、境目をぼやかして
フラクタル図形
有名なのではなくて、あまり見たことのないようなの、とか。枝葉に分かれていくTODOにどこまでも対応するマインドマップの枝のような
生物の進化
上から下に向かって。漫画みたいにせずに、図鑑以上のクオリティでないと、かえってよくない
偉人
なんの意味も説明もなく、物理学の大御所の顔写真を並べるなど
GTDカード(試行中)
こういうのを裏紙等でたくさん作っている。
真ん中に大きい丸、右に小さい丸が8個。丸は輪郭をはっきり描いてなくて、浮き出す影のような感じ。
GTD(TODO)は、時間に対して動的に変化していくため、他のカードと比較して扱いが難しい。しかし、その変化する情報・精神的な負担(覚えないといけないことを忘れることができる)も引き受けるようなカードにしたい。まだ完成しているとは言えないけれども、TODOをこなしてゆく一連の時間の変化に対応したカードを創ることはできないだろうか。
2010年11月12日金曜日
コレクト
# @CORRECT_st で、この魅力(引きつけ・アトラクト)は、「使い方」等の周辺
領域が、商売上も、重要では、と(^^ モレスキンに対するコクヨの野帳、ほ
ぼ日手帳やフラ ンクリン・プランナーに伍するPoICシステムの魅力、のよう
な・・・ about 9 hours ago webから
* 削除
#
@CORRECT_st でもPoICマニュアルのページで見る情報カードやドックって、コレ
クトのHPよりも魅力的な気が(^^;ってすみません。でも自分は「PoICマニュ
ア ル」を知った後、コレクト情報カードがPDAに匹敵する魅力あるものに見える
ような・・・ about 9 hours ago webから
* 削除
#
@CORRECT_st で、�「周辺アイテムをどうぞ」、みたいな・・・ about 9 hours
ago webから
* 削除
#
@CORRECT_st ここで「東大生」という言葉は、殺し文句!でも、情報カードっ
て、受験だけじゃなくて、もっと幅広い文句があるはず。研究者、科学者、医
者、弁護士、先 生・・・ about 9 hours ago webから
* 削除
#
@CORRECT_st その周辺に、�情報カードによる知的生産の現場の例。「アイデア
を瞬時に捉え」、「蓄積し」、「並べ替えて、創造(再生産)」。分かりやすい
具体例を2、 3程。「東大生のノートは美しい」のような。 about 9 hours
ago webから
* 削除
#
@CORRECT_st コレクトやコクヨ等が、紙やその周辺を売るとき。例えば、�「知
的生産の、本質。」とか、「想像から、想像する。」みたいな(^^;;ひ
えーっ)理念を表 すキャッチコピー。 about 9 hours ago webから
* 削除
#
@CORRECT_st で、もうひとつは、PoIC(農場)的発想で、知的生産(学術的な
場、アイデアを設計して商品化等)に、知的生産の場から逆に考えて、PCソフト
や PDAがこの20年間に栄えてきた(ハードを開発)のとは逆に、ソフト面から
考えていくと、もっと面白い方向があるような。 about 9 hours ago webから
* 削除
#
@CORRECT_st で、GTD(工場)的発想で、カード周りの販売を広げていこう、と
いうのが1つ。 about 9 hours ago webから
* 削除
#
@CORRECT_st 「Evernote」、クラウド上に、紙も電子媒体も置こう、という発
想。決して「紙を電子媒体に置き換えよう」というわけではない。 about 9
hours ago webから
* 削除
#
@CORRECT_st 上述では、決して「ソフトやPC、PDAにより自分の世界を深めよ
う」とは言っていないところが、逆に注目だと思います。 about 9 hours ago
webから
* 削除
#
ここでは、オタクと言われる岡田斗司夫が、世界を�実社会、�電脳世界、�自分
のノートの世界で考えています。で、�電脳世界バンザイ、ではな く、その先に
�実社会や電脳世界に匹敵する自分の脳内リンクの世界があり、それは紙の
「ノート」によって創られていく、と言っています。 about 9 hours ago webから
* 削除
#
@CORRECT_st でも、紙の方が上、っていう項目は、いくらでもあり、それは知的
生産においてより本質的なことに関すること。岡田斗司夫のノート術
http://otaking-ex.jp/yawa/1004_01_10.html (最初から見ないと分かりにくい
かもしれません)。 about 9 hours ago webから
* 削除
#
@CORRECT_st どちらが上というわけではないけど、今まではPC系(ハード、ソ
フト)神話が過剰で、紙のメーカーはHPを見ても、ほそぼそ・・・ってつつまし
い感じ。 about 9 hours ago webから
* 削除
#
@CORRECT_st (続き)(まあ、必ずしもそうでなく、色々なケースがあるだろう
けど)。で、コレクト社など、紙の方を売る側は、遠慮しなくていい、と思う。
本当のことを 言えばいい。世界中の人はうすうす分かっている。ソフト・ハー
ドを包含するPDAの後に紙のHipstarPDAが出てきたように。 about 9 hours ago
webから
* 削除
#
@CORRECT_st ソフトがササッと書類等を作るCMは想像できるけど、実際に�紙に
アイデアを書き、並べて、最後にPCで清書、�最初からパワーポイント、2者が
知的生産 をする過程を比較するイメージ映像があったら、実質的には�に軍配が
上がるように思う。 about 9 hours ago webから
* 削除
#
@CORRECT_st 例えば、学会発表等の準備を創るプロセスで、MSパワーポイントは
最後の2割。本質的なところは、紙でささっと描く(時間は2割、内容的には8
割)。そし て最後にパワーポイントに、いろんな図等を持ってきて貼りつけ、
全体を創っていく(内容的には2割、時間は8割)。 about 10 hours ago webから
* 削除
#
@CORRECT_st マイクロソフトなど、PCやソフトメーカーの側は、「紙よりも優れ
ている」ことを説いてきた。しかし、知的生産の本質的な部分は、1970年代
(梅棹忠夫 「知的生産の技術」の時代)から何も変わっていない(全体の8割
を占める2割の部分)。
2010年10月24日日曜日
1-1-2 カード_05
PCのキーボード入力はナイフとフォークで肉を食べる時のように、肩が張った姿勢となり、また視線は前方に行きあごが出る。一方カードへのペンによる転記は、茶碗と箸でごはんを食べる時のように、肩が落ちて、視線は下方、両手の内側になる。モバイルPCの画面と5×3カードの紙面が同等の大きさであったとしても入力継続時のストレスはカードの方が小さいと感じます。
1-1-2 カード_04
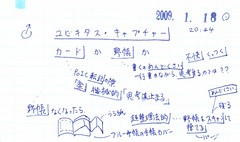
カードに直接描く場合は、転記の手間がなく楽、1項目1カードに分かれている、という特長があり、忘れないうちに(メモリが揮発する前に)急いでキャプチャーする必要があるためカードの内容(出来)はスケッチ的なものとなります。一方、野帳に記載する場合は、カードへの転記が面倒、野帳上の複数のメモは完全に分離されていない(くっついている・不快)のですが、カードへの転記はメモリの忘却を気にしなくてよいので前者と比較して清書(成書・正書・整書・聖書)的なカードが出来上がります。
1-1-2 カード_03
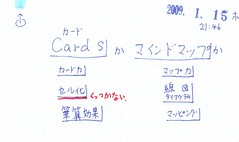
比較してそれぞれの特徴を考えてみます。
カード力は、1つ1つの項目がセル化しており、くっつかない。そろばんのような筆算効果(例.122+437=?を計算するときのやり方)が得られます。一方マップ力は、線図(ダイアグラム的)であり、くっついていること。またマッピング効果(面的に捉えられる)が得られます。
マインドマップは、前述の発散・収束の対比から見ると、発散的である(ただし、それが1枚のマップ(紙・カード)に、結果的に収まるので、一歩引いてみると、収束している)。カードは、1枚1項目の単位で見るならば、それぞれが収束的である(ただし、野帳に発想を描いている時や、直接カードに発想を描き出している状態は、発散的)。
1-1-2 カード_02
野帳へ描く作業は拡散的(宇宙に広がるイメージ・Microsoftワードの設計・欧米的)。これに対し、カードへの転記作業は収束的(箱庭を創るイメージ・初期の一太郎の画面設計・日本的)。
GTDで1つ増えたTODOリスト、これは、まだどうなるか分らない、発散的なイメージ(結論が出ていない)でしかない。一方PoICの1枚のカードは、「鏡・剣・玉」(再帰・創発・相転移)からなる1つのセット(箱庭・幕の内弁当・一匹の生き物)(結論が出ている)である。
1-1-2 カード_02
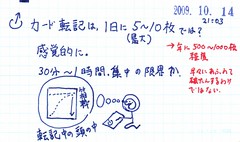
実際には、野帳からの転記で増えるカードは、感覚的に、1日に(最大でも)5~10枚では、と思います。30分~1時間が、集中の限界か。あるいは、転記中の頭の枠が一杯になってしまうからでしょうか。このペースは、年に500~1000枚程度。ドックだと1箱で1000枚入るので、早々にあふれて破綻するわけではないです。
1-1-2 カード_01
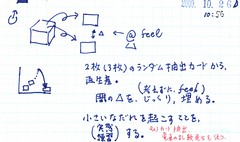
カードへの転記は、カード(細胞)が生まれるということ。その何が楽しいのか。それは「種」であり「実」であること。
「たった今描いた、3枚のカード」からでも、自分の好きな形をした再生産物が生まれるだろう、その可能性。それをみて、にんまりしたとしても、他の人からみたらそれが面白いのかどうかわからない、いや、むしろ面白いという保証は全くない(!)のですが、特に「まだ文章化されていない発想カード」・「記録や参照と結びついた発想」・「記録からあぶり出される今まで見えなかったパターン」、これらの文章化や形を見てみたいこと、それをみて自分が楽しい(内容は自分の好きな分野・ジャンルであるから)ことだけは確かです。
2010年10月23日土曜日
2010年10月15日金曜日
非線形常微分方程式
(1)とても難しくて(神様でも解けない)、
(2)とても簡単(小学生でも計算できる)
な、理由。
(1)原理的に、数式処理では解けない(数式"処理"ソフトでも無理)。
(2)だから、電卓を使って、手計算で、がりがり計算するしかない。
(これは、小学生でも出来る単純作業の繰り返し)
で、Scilab等の数値"計算"ソフトは、「がりがり」(※)と、計算してく
れる。
(※)「がりがり」とは、
�ちょこっとふやして(「足し算・引き算・かけ算・割り算」して)、
�「足し算」、
また、ちょこっと増やして(�に戻る)の繰り返しのこと。この「ちょこっと」
を、もの凄く小さい数(0.000・・・・1)とかにすると、計算回数が
1000・・・
回、という風に、もの凄く増える。だから、計算用紙がたくさん必要で、
鉛筆で何枚も「がりがり」と、書かなくてはいけない、という様子。
(メモ)
書く→(再帰・創発・相転移)→描く
□ → ○
描く→(再帰・創発・相転移)→書く
○ → □
2010年9月19日日曜日
2010年8月27日金曜日
2ブロックシステムのプログラム
function Xdot=f(t,X)
P=X(1)
A=X(2)
Z=X(3)
D=X(4)
//------------------------------------------------------
Xmat1=[
0, A*P/(1+P), 0, 0;
0, 0, 0.01*Z*0.1, 0.01*Z*0.9 + 0.01*A;
0, 0, 0, 0.1*Z;
0.01*D, 0, 0, 0
]
dX1=[
-sum( Xmat1(1,:) ) + sum( Xmat1(:,1) );
-sum( Xmat1(2,:) ) + sum( Xmat1(:,2) );
-sum( Xmat1(3,:) ) + sum( Xmat1(:,3) );
-sum( Xmat1(4,:) ) + sum( Xmat1(:,4) );
]
//------------------------------------------------------
P=X(5)
A=X(6)
Z=X(7)
D=X(8)
//------------------------------------------------------
Xmat2=[
0, A*P/(1+P), 0, 0;
0, 0, 0.01*Z*0.1, 0.01*Z*0.9 + 0.01*A;
0, 0, 0, 0.1*Z;
0.01*D, 0, 0, 0
]
dX2=[
-sum( Xmat2(1,:) ) + sum( Xmat2(:,1) );
-sum( Xmat2(2,:) ) + sum( Xmat2(:,2) );
-sum( Xmat2(3,:) ) + sum( Xmat2(:,3) );
-sum( Xmat2(4,:) ) + sum( Xmat2(:,4) );
]
Xdot=[dX1 * 0.9 + dX2 * 0.1;
dX1 * 0.1 + dX2 * 0.9]
endfunction
// 初期値
X1s=[2; 1; 0.01; 0]
X2s=[2; 3; 0.01; 1]
Xs=[X1s; X2s]
//時間
t0=0; t1=50; dt=0.01;
t= t0 : dt : t1;
//微分方程式solver
x=ode(Xs,t0,t,f)
// グラフの表示
clf()
scf(0)
plot2d(t,x(1,:),2)
plot2d(t,x(2,:),3)
plot2d(t,x(3,:),4)
plot2d(t,x(4,:),5)
scf(1)
plot2d(t,x(5,:),6)
plot2d(t,x(6,:),7)
plot2d(t,x(7,:),8)
plot2d(t,x(8,:),9)
2010年7月28日水曜日
Scilabでルンゲ・クッタ法
のでは。
つまり、解く必要がない。
欠点は、本来の解とずれる可能性があること。しかしルンゲ・クッタ法は、精度
がよい。
サブルーチンを気軽に使い回せれば。そして、
刻み幅をもの凄く小さくして(精度を上げる)、そのかわりプロットはぽつぽつ
と(PCに負担をかけない)。
(引用)
サブルーチン
http://blog.goo.ne.jp/korondemo/e/c65cbd966ee301fb22bd8ea6786060a6
実行プログラム(強制振動)
http://wavelet.blog58.fc2.com/blog-entry-141.html
http://ki-diary.cocolog-nifty.com/kiblog/2003/10/scilab_5c5e.html
2010年7月27日火曜日
2010年7月3日土曜日
シム
// 捕食 被食 死滅・沈降・溶出
A = A +( 0.2*P/(1+P)*A ) - (A * Z/V) - ( A * 0.1 ) // 藻類
D = D + (A*0.1) + (Z*0.1) + (F*0.01)-(0.1*D) // 泥
Z = Z + ( A * Z/V ) - ( F * Z/V ) -(0.1*Z) // ミジンコ
F = F +( F * Z/V ) - (F * 0.01) // 魚
P = P - ( 0.2*P/(1+P)*A ) + ( 0.01 * D ) //栄養塩(リン)
2010年5月24日月曜日
2010年5月14日金曜日
1-1-1-5-2 [創発・相転移] 構成・構造_06
砂時計で、砂山に砂が重なっていく様子。ある一定量毎に、違う色の砂を積もらせてゆき、その断面を見ると、地層の様な模様に成っているだろう。そして、その1点、例えば、砂山の形を正規分布の釣鐘曲線(ベルカーブ)としたら、そのσ(標準偏差 http://ameblo.jp/tryangle250/image-10400932377-10325520743.html )にあたる点をつないでいったら、上方に立ち上がっていく曲線も見える。
2010年5月6日木曜日
ウルフラムの軸
に、
(引用)
-----------------------------
>ただし、この本を読んでも何が限界なのか、なぜ離散化が必要なのか、どうし
てセルオートマトンなのか、なぜ方程式でなくて離散シミュレーションなのか、
わからない。ひたすらセルオートマンによるシミュレーション(実は何について
のシミュレーションだかよくわからない)だとか、時空をネットワークグラフで
表現する方法(どうして時空をグラフ化するのか理解できない)だとか、方程式
をコンピュータシミュレーションに置き換える手法(これについては全く理解で
きない)が書いてあるばかりである。
-----------------------------
とあるけれども、これの答えは、ひょっとしたら、「離散的手続きから生まれた
マセマティカが説明できることは、離散的手続きで説明できる。他方、LISP で
はないFortran等のプログラムでは方程式を扱えるのに、数学ソフトが構築でき
ない。従ってこういう原理からは物事は説明しきれない。」ということではない
かと思った。
ウルフラムは、自身のプレゼンテーションで、マセマティカと、NKSと、検索シ
ステムのアルファの3つを軸に説明している。(アルファの構築原理は分からな
いけれども、)これは、離散的手続きから、全てのことを説明し、理解する、と
いう、ある意味シンプルな概念が、その根本にあるのではないだろうか。
(2010.5.7 追加)
Re:> http://kashino.exblog.jp/2951597/
という見方は、ひょっとしたら表面的な見方かもしれない。というのは、離散や、セルオートマトンは、表面的なもので、その奥には、「”再帰的手続き”をもとにして、物事を根底から見直す」というのがある。
そして方程式による教科書的見方は、マセマティカの範疇にあり、ウルフラムの手中にあるものであるが、これを壊してまで、マセマティカのさらに根底の原理から、科学の見方を再構築する、そしてそれは、いわゆる複雑系が扱う、「物理学や生物学が取り残した複雑な分野(相互作用、気象、生態系など)」だけではなく、「物理学や生物学そのもの(!)」でさえ、再構築する、という、構造的な意味があるのではないだろうか。
2010年5月5日水曜日
1-1-1-5-2 [創発・相転移] 構成・構造_05
カードの蓄積はまた、②脳の情報の流れにも似ている。時系列で記憶がたまってゆき、それを元に発想が生ずる。
①時間が流れ、歴史(結果)がたまってゆく。
②情報が流れ、記憶(記録)がたまってゆく。
たまるにつれて、その全体の形が滑らかになって行く。砂時計を落ちる砂粒、落ちた砂粒が数粒の時は形もない、数十粒では盛り上がりができ、数百、数千で釣り鐘の形が現われる様に。
蓄積の様子のイメージを数学の記号で表すと、砂粒の数が①少ないときは、Σ□、砂粒の数が②多くなると、∫□ 。(※ここで□は粒やカードを表す)。
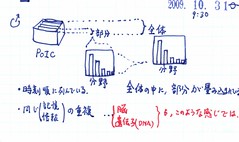
1-1-1-5-2 [創発・相転移] 構成・構造_04
一方、その一部の塊を取り出した場合にもまた、複数の分野が混在している。部分に全体の構造が畳み込まれた、フラクタルな構造の様に、一本調子でなく、ジップの法則つまりf分の1に、自分の興味ある分野のカードがゆらいで存在している(極端なものほど少ない)ので、パラパラと繰って見たとき、心地よいのではと思います。
1-1-1-5-2 [創発・相転移] 構成・構造_03
PoICで、まず最初に①ドックにカードをためていく段階では、そこに情報のレベルでの形や構造(本の「目次」の様なもの)はありません。次に②カードがたまってゆくと、ドックの容量制限から来る精神的ストレスがたまり、また、情報カード群の塊の内部の情報エントロピーもまた、増大していきます。そこで、 ③主要なカードをごっそり抜き出して、「再生産」します。ここでは、(1)分類(グループ化)と、(2)順番を決める(順列化)の2つのことを行います。
グループ化(分類)も、順列化も、単純作業の繰り返しです。グループ化は、トランプの様に、カードの束から
①1枚目のカード[カード1]を取る。
②次のカード[カード2]を取る。
③[カード2]が[カード1]と同じグループか?
YES→[カード1]の上に置く。
NO→[カード1]の隣に置く。
④次のカードを1枚取る。→(③の作業を繰り返す)。
次に順列化。一つのグループから、
①1枚目のカード[カード1]を取る。
②次のカード[カード2]を取る。
③[カード2]は[カード1]の後か?
YES→[カード1]の後ろに置く。
NO→[カード1]の前に置く。
④次のカードを1枚取る。→(③の作業を繰り返す)。
この繰り返し作業の結果、ドックの中のカード群を、「塊・かたまり」としてみるとが出来る。個人的には、初めてごっそり再生産用にカードを取り出したとき、1年間多岐に渡るカードを投げ入れていたつもりが、大きく3(~4)個の塊に分けられることを見て、驚きました。
塊の大きさは当然ですが差があり(内容の分布は均一ではない)、サイコロを多く振れば振るほど1の目が6分の1の回数に近づく(大数の法則)ようなものとはまた違う、不均一化に向かう「見えない働き」があるのかな、と思いました。
2010年5月2日日曜日
1-1-1-5-2 [創発・相転移] 構成・構造_02
以下はPoICを始めて11ヶ月程経ったときに思った、単なる個人の予想です。
人は興味があることも興味がないこともいつも均等に考えているわけではない。偏りがある。どうしてか。興味があること(アトラクター)ほど、心を引きつけるから。人の感覚(時間や、音などの刺激)はべき乗則に従う。人の興味もまた、そうなのでは。大勢の人の人気投票(Amazon.comの商品の順位と売れ行き)はロングテールの法則(Ref: ja.wikipedia.org/wiki/%E3%83%AD%E3%83%B3%E3%82%B0%E3%83%8... )に従います。
カードが1000枚まで貯まったとする。ここでカードを分類したとき、1位から4位までの分布はどのような感じになるだろうか。ロングテールの法則のようなべき乗則に従うとしたら、ジップの式(Ref: ja.wikipedia.org/wiki/%e3%82%b8%e3%83%83%e3%83%97%e3%81%a... )のようになるのではないだろうか。この式には係数がいろいろ付いていますが、それらを単純に1としたとき、
1番目に興味がある分野が全体の3分の1(34%、340枚)とすると、
2番目に興味がある分野は1位の半分(17%、170枚)、
3番目に興味がある分野は1位の3分の1(11%、110枚)、
4番目に興味がある分野は1位の4分の1(9%、90枚)、
・
・
・
こんな感じで、興味のある(心を引きつける)分野ほど多く、興味が無くなるにつれて減少してゆくのではないかな、と思いました。
1-1-1-5-2 [創発・相転移] 構成・構造_01
「時間の流れ」は、どういうイメージで表されるでしょうか。
PoICの「時空の輪」(Ref:PoICマニュアル)では、時間の流れを、「未来から現在、そして過去へ過去へと蓄積していくカードの流れ」として表されます。葉っぱのように蓄積していくカード。
ここで流れていく情報カードは、「どんな人でも、その人の持つ再帰・創発のプロセスの中から描き出されたもの」です。そして、カード群からの再生産の成果は、「どんな人でも、その人の持つ再帰・創発・相転移のプロセスから磨き出されたもの」といえます。それは、「その人が、他の人には置き換えのできない、その人のオリジナルとして、伍していける(可能性のある)もの」なのでは、と思う様になりました。
2010年4月30日金曜日
自己組織化によるプラズマ中の構造
(引用)
①>我々の生活に必要不可欠な火(燃焼炎)もプラズマの一種である。
②>自己組織化によってプラズマ中に生成されるさまざまな構造
>フィラメントや渦といった構造は、条件が整うとお互いが生み出した磁場によって、同じ方向に動いているほかの渦を引き寄せて、自己組織化しながら成長していく。プラズマは螺旋状の渦を作ったり、一定条件下では渦糸が結晶構造を作ることもある。渦の成長はやがて止まって何らかの理由で自然消滅した後に、再び新たなフィラメントを生 成ていくこともある。このような生成と消滅を伴うエネルギーのサイクルは、グレートウォールとボイドによって構成された、銀河の集団が作る気泡状の宇宙構造が生成されていくメカニズムの中にも認められる。
(Ref:Wikipedia)
追加(2010.5.3)
Hawk氏のBZ反応 http://pileofindexcards.org/blog/2009/09/06/belousov%E2%80%93zhabotinsky-reaction/ と、「火」と「宇宙の構造」は同じ
その理由:「反応と拡散」の中で、自己組織的に「渦」構造が形成されるから
1-1-1-5-1 [創発・相転移] 蓄積_04
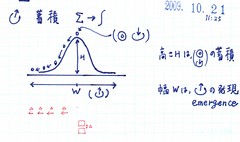
砂粒の高さ方向への蓄積量(高さH)は、後の再生産の材料になる記録(◎)、参照(↓)あるいは発想(!)カードの蓄積枚数を表す。こつこつと、時系列に従って、積み上がっていく。
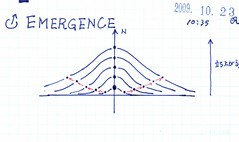
この砂山の幅Wは、積み上がったカード(◎、↓、!)から新たな発想(!)が生じたときの雪崩により広がる。すなわち、幅は発想の新たな出現(emergence)を表している。
砂山の形は、①積み上がってゆき直線に近い形を表して行き(再帰・鏡)、②ちょこちょこと現われる小さい雪崩により頂上が丸くすそ野が少し広がったロケットの様な形をおびていき(創発・剣)、③「ざざーっ!」という大きな雪崩により、高さと幅を持った釣り鐘の様な形が現われる。(相転移・玉)。
この山の形は正規分布( ja.wikipedia.org/wiki/%E6%AD%A3%E8%A6%8F%E5%88%86%E5%B8%83 )と呼ばれ、「π」や「e」という不思議な数を使って表される。
2010年4月29日木曜日
1-1-1-5-1 [創発・相転移] 蓄積_03
「こつこつ」貯める、とは、砂山に粒を落としていくこと。これは、PoICで、ドックにカードを貯めていく事と同じ。そして、その面白さは、直線的な増加(すなわち、10枚描いたら10枚貯まる、20枚描いたら20枚貯まる、というような、努力に応じた増加)にあるのではなく、貯まると雪崩(なだれ)という、動的なイベントが起こることにある。
心を動かされるのは、この「ざざーっ」という瞬間。ろうそくの場合は、炎。雪崩が起こる前の状態は、ろうが溶けて、高温の臨界状態(反応前)。雪崩は、発火して、炎が上がり、ろうの分子がプラズマとなり光を放つ瞬間(新しい状態・もの・イベントの出現)。雪崩が落ち着いて裾野が広がった状態は、ろうが灰や CO2になり終えた静的な状態。
1-1-1-5-1 [創発・相転移] 蓄積_02
このときの、カード数の増加と、組合せの増加、そしてそれに伴う「感覚の高まり」は、片対数グラフ状の直線に似ている。横軸はカードの枚数の増加を示す。グラフの軸は、通常の軸(線形軸)。縦軸は、カード間の組合せの増加を示し、これを対数軸で表す。縦軸の値は指数的に増加していくが、これを対数軸の枠に押し込める。カード間の組合せが増える感覚が、10から20に増えるとき(2倍)と、100から200に増えるとき(2倍)とで、同じに表される。
感覚は、対数的に感じられるものが多い。例えば、カードの枚数、カードの組合せ、音の周波数(ピアノのドレミ)、時間の経過。
2010年4月25日日曜日
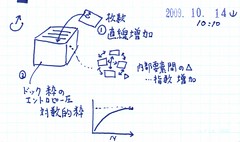
1-1-1-5-1 [創発・相転移] 蓄積_01
一方、内部要素間のΔは指数的に増加。
②ドックの収容力(定員)には限りがある(1000枚程度)。増えるにつれて、増加に対する圧力が増加していく。
環境収容力(個体数の制限)があるときの生物の増加の様子を表現するために、ロジスティック式( http://ja.wikipedia.org/wiki/%E3%83%AD%E3%82%B8%E3%82%B9%E3%83%86%E3%82%A3%E3%83%83%E3%82%AF%E5%BC%8F . )が考案された(1838年)。この式によると、
生物の増加速度=r(定数)×(定員数-生物数)×生物数
という形をしている。ここで(定員数-生物数)という項目がある。この値は、生物数が定員数に近づくほど0に近づく。つまり、定員数に近づく程、増加にマ イナスの圧力が働くことを表している。そして定員に達すると、(定員数-生物数)は0となり、増加速度も0となる(増えなくなる)。
この概念をPoICのようなカードシステムに当てはめてみる。箱(PoICではドック)の定員数(容量)を1000枚とすると、1000枚に近づくほど、カードの増加速度を鈍らせる要素(精神的な制限など)が増加する。
2010年4月23日金曜日
2010年4月18日日曜日
気にせず進む
http://kazuschool.blog94.fc2.com/blog-entry-74.html
カードをまとめるのも、次があると思って気にせず進めることにする。
章毎の再生産的な文章は概ねできているけど、今、1枚1枚のカードを御役後免にする前に、一時的にテキスト化した文章を、カードと対応させて、隙間を埋めていく。
後でWiki化等するときに、個々のカードは章の下の節やコラムのような位置づけで。
また、完成した後、テキストで個々のカードまで全文検索が出来る。これは、「ノート1冊」法が、ノート毎に索引を作るから検索が出来る、というのに対して、PoICの場合は、再生産しているから、再生産物そのものがデジタル上に置いておけば検索できる、というのに対応している。
1-1-1-4-2 カード間の相互作用_12
カード間のΔの個数の、潜在的な可能性。
カードが10枚のとき、45個。
カードが100枚のとき、4千個。
カードが1000枚のとき、45万個。
10C2 = 45 (約50)
100C2 = 4,450 (約5千)
1000C2 = 459,500 (約50万)
例えば、カード50枚では、50C2=1,225個(ドック1箱分)。
1-1-1-4-2 カード間の相互作用_11
(※このカードは、既存の2枚のカードを組み合わせて描いたものです。)
1-1-1-4-2 カード間の相互作用_10
文書や知的生産物を組み上げるとき、1つ1つの単位となる粒の「大きさ」を、活字ではアルファベット「1文字」にしている。京大カードや情報カードでは、「1発想」(記録、TODO、参照)を最小単位としている。
活字が、①集まって、(再帰)、②単語の方針ができ(創発)、③文章ができる(相転移)。
カードが、①集まって(鏡・雲)、②方針ができ(剣)、③文章ができる(玉)。
1-1-1-4-2 カード間の相互作用_09
①反応性のある粒を1カ所に集める
②1粒を反応させる
③高温が出る
④別の粒が反応する
⑤→③に戻る
PoICの場合も同じで、①反応性のあるカードをドックに集めて、②反応させる。
炎の場合は、粒が一定以上になると(臨界点を超えると)、上記の③から⑤のサイクル(連鎖反応)が、自動的(自発的)に繰り返される☯。臨界点(閾値)は、粒の数で決まる。
[臨界点・炎・連鎖反応] ≒ [Δ・カード間からの新カード生成]
ここで、N枚のカードがあるときの2枚のカードの間(Δ)の個数(組合せ)は、関数電卓では、組合せ(コンビネーション)nC2で計算されます(例えば、50枚のカードがあるとき、HP製関数電卓では、[50]、[2]、[C]とキーを押すだけです)。
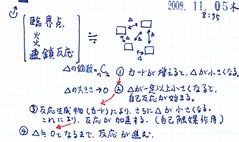
カードの数が増えると、何が起こるでしょうか。カード間の距離が小さくなり、反応が起こりやすくなります。
①カードが増えると、Δが小さくなる
Δの大きさ→減少する(0に近づく)
②Δが一定以上小さくなると、自己反応が始まる(勝手に反応する)
③反応生成物(カード)により、さらにΔが小さくなる
これにより、反応が加速する(自己触媒作用)
④Δ≒0となるまで、反応が進む
1-1-1-4-2 カード間の相互作用_08
なお、頭の中でもまた、同様のプロセスが生じているのではないだろうか。個々のカードは、海面の光の反射のような、模様で。
1-1-1-4-2 カード間の相互作用_07
カードが直線的に増加すると、その組み合わせ数は、(直線的ではなく)曲線的に増加する。
カード間の差Δ(カード間の濃度勾配・落差、気圧差・温度差)の「数」は、曲線的に増加していく。
1-1-1-4-2 カード間の相互作用_06
カードが2枚だと、より多い場合に比べて、Δが見やすい。
(※このカードは2枚のカード [09/02/08/00/45] および [09/10/13/09/50] から描かれました。)
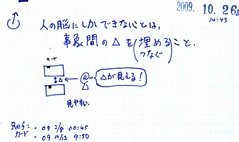
1-1-1-4-2 カード間の相互作用_03
間のΔを、「感じて」、じっくり、埋める。
小さい雪崩を起こすことを、実感(練習)する。
笑点(番組)や、謎掛け(「○○と掛けて、□□と解く。その心は?」)と同じ。
これが現段階では、機械では出来ない。粒やブロックのような固い物からは、なかなか出来ない。波や粘土のような柔らかい物からは、ぐにゃぐにゃと出来るのだけれど。
2010年4月17日土曜日
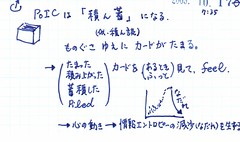
1-1-1-4-2 カード間の相互作用_02
ものぐさ、ゆえに、カードがたまる。
たまった(積み上がった・蓄積した・Piled)カードを、ある時ふっと、あるいはよっこらしょっと見て、何か感じる。そして心の動きが、雪崩(情報エントロピーの減少)を起こす。
1-1-1-4-2 カード間の相互作用_01
他方、HAL9000型のクローズなデータストック型のシステムとして、PoICが生まれました。
1-1-1-4 再生産 タスクフォース編成_05
これらの方法(ノートやデジタル機器)からでも再生産できる。例えばノートをバラバラにしたり(Ref:Hawk氏のTwitterでのコメント)、ノートやデジタル機器の情報をカードに書き写したりプリントアウトしてPoICすればよい。
1-1-1-4 再生産 タスクフォース編成_04
1ヶ月にたまった100枚のカードでブログやコラムを。(※カードは戻す)
3ヶ月にたまった300枚のカードでWikiを。
1年にたまった1000枚のカードで本のような塊(魂)を。
なお、実際に100枚のカードを目の前にすると、その情報量は膨大な量で、1つのブログには収まりきらないものであることが分かりました。
2010年4月11日日曜日
ハッブル宇宙望遠鏡
Twitterに感想を書いてたら、1行書くつもりが長くなりました。文字制限があるので、くどい文章だったりしている。
ちょっと後で自分で見るために、何も考えずに貼り付けてみるテスト(ただ単に機械的に場所を選択してコピー&ペースト)(下から時間順)
--------------------------
- kf3333 (続き)・・・みたいなことを思うきっかけになって、やっぱり面白い 番組だった。 26 minutes ago via web
-
 kf3333 少なくとも、今回の宇宙の最初の歴史を数式でシミュレーション計算し た人とかは、「宇宙の熱的死」は考えていないだろうし、逆に、「熱的死」は、シミュレーション計算の式を省きまくって、たった1個の要素で考えたに過ぎな い。 28 minutes ago via web
kf3333 少なくとも、今回の宇宙の最初の歴史を数式でシミュレーション計算し た人とかは、「宇宙の熱的死」は考えていないだろうし、逆に、「熱的死」は、シミュレーション計算の式を省きまくって、たった1個の要素で考えたに過ぎな い。 28 minutes ago via web -
 kf3333 (続き)で、どうして「熱力学第二法則から導かれる宇宙の熱的死」み たいな仮説が信じられているかというと、ピストンの中のガスのふるまいのみを拡大して解釈したからであり、ピストンの中にない長時間の、膨大な原子の、ゆ らぎによる凝集、という作用を見落としていたから、で、(続く) 31 minutes ago via web
kf3333 (続き)で、どうして「熱力学第二法則から導かれる宇宙の熱的死」み たいな仮説が信じられているかというと、ピストンの中のガスのふるまいのみを拡大して解釈したからであり、ピストンの中にない長時間の、膨大な原子の、ゆ らぎによる凝集、という作用を見落としていたから、で、(続く) 31 minutes ago via web -
 kf3333 (続き)①と②の両方の作用が基本にあり、これが陰陽図や Trinityみたいに、相互に生じ(①が極まれば②となり、②が極まれば①となる)、その①と②の間の状態は「ゆらぎ」として表される。つまり熱力学第 二法則だけで宇宙の将来を考えるのは、片手落ち(続く) 33 minutes ago via web
kf3333 (続き)①と②の両方の作用が基本にあり、これが陰陽図や Trinityみたいに、相互に生じ(①が極まれば②となり、②が極まれば①となる)、その①と②の間の状態は「ゆらぎ」として表される。つまり熱力学第 二法則だけで宇宙の将来を考えるのは、片手落ち(続く) 33 minutes ago via web -
 kf3333 (続き)密度ゆらぎが生ずる。つまり、宇宙は、一方的に均一になる 「熱力学第二法則による熱的死」だけで説明できるのではなく、①「各原子が、等速直線運動により、統計的にバラバラになる方向・作用」(エントロピー増 大)と、②「重力により凝集する作用」(エントロピー減少)(続く) 35 minutes ago via web
kf3333 (続き)密度ゆらぎが生ずる。つまり、宇宙は、一方的に均一になる 「熱力学第二法則による熱的死」だけで説明できるのではなく、①「各原子が、等速直線運動により、統計的にバラバラになる方向・作用」(エントロピー増 大)と、②「重力により凝集する作用」(エントロピー減少)(続く) 35 minutes ago via web -
 kf3333 (続き)特に不均一な密度の大きい部分が出来て、それが凝集し、さら に重力の凝集作用が加速され、核融合。つまり、もともと均一(熱的死)と考えられる130~140億年前からでさえ、不均一な筋状、膜状の、密度ゆらぎが 生じた。これが遠い将来、均一になっても、さらに遠い将来、(続く) 38 minutes ago via web
kf3333 (続き)特に不均一な密度の大きい部分が出来て、それが凝集し、さら に重力の凝集作用が加速され、核融合。つまり、もともと均一(熱的死)と考えられる130~140億年前からでさえ、不均一な筋状、膜状の、密度ゆらぎが 生じた。これが遠い将来、均一になっても、さらに遠い将来、(続く) 38 minutes ago via web -
 kf3333 (続き)これは、等速直線運動をしている。どれかとどれかがぶつかっ たら、ビリヤードの玉みたいに、はねとばし合う。すると、膨大な数の何億何兆分の1かは、重力で近づき、もやもやと近い空間に集まり、自ずから重心の位置 に引き合い、集合し、一定以上集まると重くなり、やがて全体の中で、(続く) 41 minutes ago via web
kf3333 (続き)これは、等速直線運動をしている。どれかとどれかがぶつかっ たら、ビリヤードの玉みたいに、はねとばし合う。すると、膨大な数の何億何兆分の1かは、重力で近づき、もやもやと近い空間に集まり、自ずから重心の位置 に引き合い、集合し、一定以上集まると重くなり、やがて全体の中で、(続く) 41 minutes ago via web -
 kf3333 ということは、(もともとピストンのエンジンから始まった)熱力学第 二法則を、宇宙全体の空間と遠い将来への時間に適用した、「熱的死」は、起こらないのではないか。本当に均一にならない限り、そして、なったとしても宇宙 空間におよそ1Lに1個といわれる(要確認)水素分子、これは、(続く) 43 minutes ago via web
kf3333 ということは、(もともとピストンのエンジンから始まった)熱力学第 二法則を、宇宙全体の空間と遠い将来への時間に適用した、「熱的死」は、起こらないのではないか。本当に均一にならない限り、そして、なったとしても宇宙 空間におよそ1Lに1個といわれる(要確認)水素分子、これは、(続く) 43 minutes ago via web -
 kf3333 ハッブル宇宙望遠鏡の感想 従来から言われている「宇宙の熱的死」と いう考えは、やはりおかしいのではないだろうか。宇宙が始まってから、何億年かは、闇の世界、すなわち、死んでいる。しかし、その後、何億年かかけて、密 度のゆらぎを、重力が加速して、高密度の領域が出来て、星が誕生した☆ about 1 hour ago via web
kf3333 ハッブル宇宙望遠鏡の感想 従来から言われている「宇宙の熱的死」と いう考えは、やはりおかしいのではないだろうか。宇宙が始まってから、何億年かは、闇の世界、すなわち、死んでいる。しかし、その後、何億年かかけて、密 度のゆらぎを、重力が加速して、高密度の領域が出来て、星が誕生した☆ about 1 hour ago via web
2010年4月10日土曜日
1-1-1-4 再生産 タスクフォース編成_03
タスクフォースを編成すると、今までの時系列配置が崩れるので、心理的抵抗があるのですが、このカードはまとまって、お役御免カード置き場(100円のBOXやコレクト製カードケース等)へ保存されます。そして日付、タイトル、お役御免カード置き場を記した1枚のカードとなり、ドックにカードが1枚増える(成仏する)。
再生産したカードが1枚のカードに収束してゆく。
1-1-1-4 再生産 タスクフォース編成_02
タスクフォース編成を、最後に行うのが、原則だと思います。このとき、PoICの過程では、再生産の時期は想定外で、時間が過ぎてゆきます。1サイクルが、概ね1年単位の時間スケールです。
一方、テーマが限定されている場合は、有限の時間内(1ヶ月先等)に再生産することを想定しながらカードをためていくのもあるように思います(例.英語の勉強)。
接続詞
(引用)
-------------------------------------------------------
あるとき、
「接続詞」「接続語」に注意することで大幅に
喋りやすくなることが判った。
つまり、
「というのは」「でも」「そこで」「たとえば」
「別の方法として」「試しに」「この中で唯一」
っていうような言葉。
ref: http://blog.livedoor.jp/codran/archives/50907506.html
1-1-1-4 再生産 タスクフォース編成_01
言い渡すのは、エントロピーが増大し、極相に達したとき。
この時期の前後の様子について、現時点(2010.2.16)での様子を例に、描いてみます。ドックには時間順にカードが並んでおり、ちょろちょろと見たりするのは楽しく、1月に、大々的に、この順を崩すのは精神的に抵抗がありました。またその時点での当該の興味のあることについては、依然としてカードが増加し続けている状態であり、自分的には行き着くとろこまで行っていないのに、今再生産する、というのも中途半端な感じがしました。
そして、にもかかわらず、再生産のために、カードをごっそり抜き取りました(2010年の正月)。最初のカードを机の上に置き、次のカードを、1枚目に関連していればその上に、分野・ジャンルが違えば、隣に置き、また3枚目を置き・・・これを繰り返していきました。
①1枚取り出して置く
②次を取り出す
③前のと同じグループか?
YES→そのグループに置く
NO →新しいグループを作る
④「②」にもどる
ドックからカードがごっそり無くなりましたが、この頃になると、実際はカードがたまる早さが早く(といっても自分の場合は1日4枚くらい)、月に100枚くらいの束になり、野帳に残っているカード化できていないネタ(種)も集めると膨大な量であることが予想されます。
一方テキスト化等を始め、PCのアウトライナーソフトに入力していってみると、再生産物のボリュームが自分の予想とは桁違いに多いことが分かりました。これだと、たった1ヶ月にたまる程の100枚のカードから出てくる再生産物でさえ、もの凄く多いことが予想されます。これならば、実際はカードをどんどん再生産しても、それ以上に増加による補充があるから、いいのではないか、再生産はどんどんやっても、全然追いつかないのではないか、と現時点では思っています。
1-1-1-3 学習_12
それは、参照カードを、まとめると、それが自分の発想になる(発想を生じさせる)ので。
例えば、ドックの情報エントロピー圧が高まったとき(臨界状態)など。
参照カードは、発想カードに比べてたまる速度が遅い。たまって反応して相転移(「あ、そうか!」化等)するのを待つ。たまると高濃度のウラン(臨界状態)に、自ずから成る。
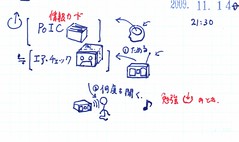
1-1-1-3 学習_11
「PoIC・情報カード」≒「エアチェック・カセットテープ」
なお、曲は、勉強の時に、何度も聞いていたものが、20年経っても忘れていない。