2010年3月28日日曜日
指紋
------------------
「指紋はなぜ渦を巻いていたりするのでしょうか?」
http://oshiete1.goo.ne.jp/qa2931075.html
------------------
(引 用)
------------------
Q 指紋は何のためにあるの?
A 指紋は、指先を敏感にすることと、物をつかみやすくするためにあるのです。
指先には、圧力などを感じる感覚点と神経がたくさん集まっています。もしも指の表面が平らであれば、ものすごく小さいものをつまんだ場合、そのまわりもへこんでしまうので、微妙な大きさや強さがわからなくなります。
しかし、指紋があることによって、山の部分だけがへこむので、非常に細かなところまで大きさや強さが感じられるのです。
また、指紋には滑り止めの役割もあります。
指紋はデコボコしているので、物に触れたときの摩擦(まさつ)が大きくなり、滑りにくくなるのです。
http://www.tv-osaka.co.jp/qsience/q_science/img/gimon_img/g_q_a/g_sei_34.html
-------------------
公園を散歩していて、指を見ると指紋があった。
渦を巻いている理由を調べようとして、「指紋 渦」で調べたら、上記の様に述べられていました。
昔、小学校の時にも、同じような説明を聞きました。
そして、分からないのは、
「Q 指紋は何のためにあるの?」
「A 指紋は、指先を敏感にすることと、物をつかみやすくするためにあるのです。」
指紋は結果として、Aの様な効果があると思います。
しかし、どうして渦を巻いているのか。どういう機構で渦が生み出されたのか。
「何のため」→「滑り止め」という意図や意志について、何が、そう考えたのか。そして、「滑り止めが欲しい」と考えたとして、それが、遺伝子レベルで発現するのか。DNAが渦を描くのか。そんなことってあるのだろうか。
多分、違う(とここでは思う(だけ))。Aの滑り止めや神経を敏感にするために、渦模様を描く、というのは、無理がある(と思う)。そんな「滑り止めが欲しい」という要求を遺伝子レベルでかなえるんだったら、もっと欲しい機能が一杯あるはず。
神経と渦は関係しているだろうけど、もっと根本的なところでつながっている(と思う)。
----------------
体の表面は神経。それが形成される過程は、カルマン渦のパイこね変換。
と{複合系・Trinity}的考えると、すっきりする感じがする。
滑り止めは、結果的な、二次的な効用で。猿は握力が凄いので、もし指紋が無くても、木にぶら下がっていただろう、ということで。
1-1-1-1 ためる_04
量の疑問と、質の疑問。
量的には、破綻。
質的には、「カードが増える」ことと「楽しい」ことの間の関連がイメージ出来ないこと。
小学校の時から、授業を受けたら、ノートに文字を書きてゆき、それによりすなわち字を書いた紙が増えていきますが、ノートが増えても楽しくないし、充実感も満足感もないです。それを、ましてや、1枚のカードに1つづつ、事項を書いていったら、一言メモの膨大な紙の束になって、あっという間に収拾のつかないことになるのではないか。
実際に行ってみると、量的な疑問に関しては、野帳にどんどんメモが増えるのですが、転記で1日に増えるカードの枚数は数枚~10枚弱、このペースだと、1000枚に達して箱がパンクするまでに1年もかかる。そして質的な疑問に関しては、カードの内容が、だんだんと、自分の「好きな」ことになってゆく、これは自分にとって「面白い」カードが増えていくこと。自分の見たいこと、知りたいことを描いたカードが増えていく。
1枚1枚のカードは、それ自体が発想等であり、自分にとって、単なる「字を書いた紙」ではなく、「有機的な情報」に見えます。そして、それが、将来、他のカードと有機的につながって、別のものを生み出す元になる、そういう「種」が増えていく、これは、自分の好きなものをためてゆく楽しさです。
コンパス
手続き。棒が1本あって、
①少し角度が増える
②わずかな円弧が描かれる
③ →①に戻る
の、手続きの繰り返し
------------------
http://www.flickr.com/photos/hawkexpress/4166325426/
も、手続きの繰り返し
------------------
円弧を、コンパスの描く円弧としてみると、これ以上ないくらいシンプル
その円弧を、四角いグラフ用紙のxy軸からみると、複雑、というより複合、すなわち①「単純なルール」の②「繰り返し」になる。
単純なルールを繰り返して、そこに弧が現われる。
再帰と創発。
その形が「円」になる。
相転移。
------------------
棒を一本、「片方を固定して、もう一方を動かす」という「操作」から、「円」という形が現われた。
2010年3月27日土曜日
1-1-1-1 ためる_03
最初は「ほんとかなあ」と思うのですが(例えば、時間順に配置しても、人の頭は、7日前の食事を思い出せない)、図書館的な分類もまた、必ず破綻する、ということで、分類は、「出来ない」(不可能)ということです。
では、何度も使うカード(電話番号など)は、どうするか。「超整理法」では神様ファイル、「PoIC」では神様カードとして、「聖域」に置く、としています。実際には、神様カードは、多くとも全体の10分の1以下(経験則)であること、記録・参照カードであることから、全体の10分の1程度の領域を、「聖域」とし、そこに置けばよいと考えられます。
「疑問」も「発想」
「疑問」も「発想」
「疑問」こそ「発想」
「疑問」から、「再帰・創発・相転移」が生まれる。
「疑問」は、いつも生まれる。すぐ生まれる。本を読んだら生まれる。
すなわち、野帳には、「疑問」から生まれた「発想」が、いつも生まれ続ける。
野帳の「発想」は、1日にどんどん、いくつも、追いつかないくらいに、継続して、増え続けている。どうして、そんな現象が起こるのか。
それは、すぐに「疑問」が浮かぶからであり、野帳にどんどん「発想」が増え続けるのは、自然で、当たり前のことである。
----------------------
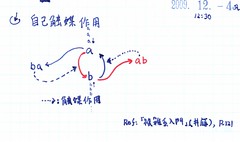
「疑問」を、客観的に、反射{ピンポン・お手玉}させる
----------------------
(引用)
ライプニッツ「役に立たないパラドックスは無い」(チャイティン「知の限界」)
http://www.unfindable.net/~yabuki/article/unknowable/ミンスキー「ゲーデルはLispを思いついておくべきだった。もし彼がLispを思いついていたならば彼の不完全性定理の 証明はもっと簡単なものになっただろう」(ホフスタッター「メタマジック・ゲーム」)
1-1-1-1 ためる_02
・情報エントロピーの減少
・再生産
・虚数
というテーマに大きく分類されてゆきそうな感じがします。
ちなみに、これらは、ブログ Pile of Index Cards やPoICマニュアル中の気になった言葉や分からない単語、面白そうな概念という共通点があります。
(※これは2009年10月16日時点で描いたカードですので、今後、より長い目で見たときは、変わってゆくと思います。)
1-1-1-1 ためる_01
その後、8月31日(ドックが一杯)に向かい、プレッシャー(エントロピー増大圧)がかかってゆきます。配列はバラバラ(時系列)であり、情報エントロピーが増加してゆきます。
2010年3月26日金曜日
ノートで検索した結果
(引用)
□□□どんなノート作ってる?□□□
- 40 :天使m:03/06/15 05:38 ID:???
- ひろし君とちょっとドジな犬型ロボットが思った疑問を
物知り博士が答える、という形でノート書いてる。
2010年3月21日日曜日
スロー
(引用)
私たちは時間を消費する線のようにとらえています。
「時間がもったいない!」「もっと急げ!」「早くしろ!」と急き立てます。
http://www.earthinus.com/2010/03/slow-is-faster.html
----------------------
これは、ひょっとしたら、{Trinity・陰陽・鏡剣玉}のらせん的に時間を過ごすこと、
1枚づつ蓄積してゆくこと、を言っているのかもしれない。
2010年3月20日土曜日
分岐
さらに、人の体、骨格も、枝分かれと見ると、似ている。
人や、骨格を持つ動物は、恐らく、球形、楕円型、卵型のような、胎児や猫が丸まった形、これが基本で、
この表面に、鶏や爬虫類の場合、表面にカルシウムの殻が、均一に分散している、これが、不均一に、丸く覆うように、枝の分岐のようなゆらぎをもって、集合している、
冬の窓の分岐する霜のように
そして傘の骨組みのような骨になる
そして、「手」と「全身の骨格」が似ているるのも、偶然ではなくて、
両方とも、丸まった形(胎児とじゃんけんの「グー」)が基本で、
この骨格が開いたのが、二本足で立った姿と、じゃんけんの「パー」
で、この骨組みの分岐は、同じ再帰的な仕組みで起こっているから、体とての骨は似ている。
物凄く単純な、再帰的な式から生ずる、マンデルブロ集合の黒ひょうたんで、体と手の比率くらいで、左右対称な全体と、やや非対照な部分が、現れるように。
○親指と頭
○人指し指・小指と両腕
○中指・薬指と両脚
これらは、その長さの比率が似ているだけではなく、肘や手足首の分岐、
そしてその神経的な敏感さまで似ている。
頭→腕→脚
そして一番先に、
つまり頭の親指、手足自体を表すところに、さらに枝分かれ構造があるのではなくて、
再帰的なパイコネ変換写像、陰陽のマークやコーヒーのミルクを少しだけかきまぜたような、指紋があるのも面白い。
頭のつむじから始まって、全身をとおって、手足の指先の指紋に螺旋が繋がる
恐らく指紋は、言われるような単なる滑り止めではなく、
全身が一つの再帰的な仕組みから成り立っていることと関係しているのでは。
(余談)
全身を統一させるのはこの指紋の渦の方向がいいのでは。
バイオリンの手、フレミングの左手の法則、女子高生の鞄の持ち方、空手の三戦立ち、大気拳など。
腹も、内から外へ手を軽く握るとどこまでも力が入るけど、逆だと緩む。
2010年3月18日木曜日
非線形
まんじゅうの「個数」が増えると、それに伴って、「総重量」が増える。
1個、2個、3個・・・
10g、20g、30g・・・
個数に伴って、重さが。
直線的に。
ところが、直線的でない増え方がある。
これは、内部に向かう増え方。
たとえば、紙を折っていくと、
1回、2回、3回・・・
分けられるブロックは、
2、4、8、・・・
折り方によっては、違った増え方をする。
折る回数と、部分の個数は、直線的な関係にない。
横軸に折る回数、縦軸に部分の個数をとると、曲線になる。
ボールの間の線の数も。
ボールが1個、2個、3個、4個、5個・・・
間の線は、0本、1本、3本、6本、10本、
横軸にボールの個数、縦軸に個数をとると、曲線になる。
これは、nC2 で表される。
-----------------
(余談)
ここで、「nC2」と、一口で言ってしまっていいのだろうか。
「ボールの間に線を引く手」として、理解した方がいいのではないだろうか。
「nC2」は、その先にある表現形式だけれども、
「一つの数式」
と見るより、
「プログラミング的な手続き」
とイメージした方がいいのでは。たとえば、「Σ」のように。
計算結果は、関数電卓で一瞬にして出るけれども。
-----------------
有限の中で、指数的に、無限に近く、増えてゆく数。
フラクタルもそう、もっと簡単に、ものさしの「2」と「3」の目盛りの間の、刻みの数。
-----------------
「非線形」というと、「線形じゃない」と言っているだけで、
じゃあ「非線形」そのもののイメージは、というと、よく分からない。
「複雑系」と言う言葉は、Hawk氏の提案により、「複合系」と言い換えると、その意味がもの凄くシンプルになり、構造もイメージできる。
すなわち、
目に見える物質から考えると、
複数の構成要素の「複合系」であり、
目に見えないその構造から考えても、
その構成要素の相互作用が、「再帰・創発・相転移」という構造をもつ、
という、
いずれも、複数(少なければ数個)の「構成物」からなる「複合系」
その振る舞いは予測できないほど「複雑」だけれども、それは結果に過ぎない。
惑星の運行、太陽系の、主要な天体、例えば、太陽と、月と、木星、これらから、地球が受ける影響、それによる起動のズレ、これは難しすぎて予想もできないと言われたほどだけれども、
たった4つの天体が、お互いに引力で影響を及ぼしながら、動いているだけ。
「複雑系」というよりも、「複合系」
--------------------------------
(引用)
www.a-phys.eng.osaka-cu.ac.jp/suri-g/phys8.html
>彼(ポアンカレ)は、連星と呼ばれる2つの星のまわりを回る惑星の運動(3体問題ともいう)は、万有引力項を持つニュートンの運動方程式で記述されるがその軌道はあまりにも込み入っていて図を書くことさえできない、と述べています。
--------------------------------
「非線形」と言う言葉についても、その基本は、一方が足し算で増えたとき、他方がそれとは違った増え方(かけ算や、かけ算の「回数」など)をする、
それを方眼紙にプロットすると、曲線が現れる(「非線形」)、
その構造は、粒(粒子、単位)の相互作用や、粒間を結ぶ線の本数、粒間の組み合わせなど、内側に向かって、爆発的に増えたり、0に近づいたり、一定値に収束していったりする。
有限の中から、内に向かって、「無限」の影が現れてくる。
2010年3月17日水曜日
リンゴ
www.vl-o-lv.com/apple/land/apple4_l.jpg
-----------------------------------
植物の経路
葉 直線的な再帰的発展
「ト」の形の、直線的な再帰的繰り返し
花 回転
葉のような構造体(花びら)が、2次元的に回転する
実 花のような構造体が、3次元的に回転する
花がくちゃくちゃっと丸まる
らせん
---------------------------
(引用)
www.hypernumber.net/wp-content/uploads/mikan_ hukuro_ringo...
---------------------------
植物は、
種が、細胞を増やして(再帰・鏡)、
上(幹)下(根)に伸びて(創発・剣)、
花・実がなる(相転移・玉)
という、{Trinity・陰陽・複合系}的発展をし、世代が繰り返す。
---------------------------
そして、その構造も、
幹、花、実、と、それぞれ、再帰的繰り返しにより、デザインされる。
---------------------------
ウルフラムの、「A New Kind of Science」では、幹と花について、述べられている。
そして、実については、電磁波やツイスター的な形、中心に角運動量をもって回転しながら直進す る粒子の周りの波紋、この波紋は、近接作用によって、1層1層、増えていく。
その断面の形は、リンゴに似ている。
あるいは、みかんに似ている。みかんは、皮をむくと、房に分かれている。
この房は縦方向に分かれている。ツイスターだと、縦向けの方向に筋が描かれる。
島構造 -箱庭-
図3 標準写像のポアンカレ断面と島構造
http://www.a-phys.eng.osaka-cu.ac.jp/suri-g/phys8.html
は、細胞をスライスした顕微鏡写真に似ている。
http://jsp.umin.ac.jp/corepictures2007/07/c01/large/FILE0003.JPG
同じところに細胞内組織が「たまる」様子。
-----------------------------
(引用)
>ヘテロクリニック構造に対応したカオスの海(銀河のようなバラバラの点の集合)とトーラス(周期的あるいは準周期的な規則軌道)は相平面上に住み分けて共 存しています。
>また、トーラスの周りのカオスの海には微小トーラスの島構造ができ、さらにその周りにより小さなスケールの島構造ができてフラクタルな構造 が生成しています。
-----------------------------
「細胞」は不思議である。その
①「構造・セル」と
②「機能・生きていること・強調して連動しているように見えること」
このうち、①については、「カオスの発生」という、「非線形」数学から、決定論的に、導かれることが、この図により分かる。
この分野は、もともと、惑星の運動が予想よりずれ(3体問題)、これが計算では予測できないほど複雑であることから、検討がスタートしている。
世の中の多くの物事は、「3体問題」(実際は3以上)である。とても予想はできなさそうに見える。しかし、「ある一定の範囲内に、納まる」様子は、無限大や無限小に発散するのではなく、ある範囲内にある、ということを意味する。箱庭的。
ものさしの、2cmと3cmのメモリの間に、無限の実数の長さが存在するように。
2010年3月14日日曜日
うどん
うどんは、一説には、弘法大師によりもたらされたものであり、
「混沌(こんとん)」→「温沌」→「うどん」
となった、という。
「カオス」→「うどん」
------------------
Wikipedia(うどん)でも、以下の様な記述があります。
(引用)
>奈良時代に遣唐使によって中国から渡来した小麦粉の餡入りの団子菓子「混飩(こんとん)」に起源を求める説もある。
>平安時代に空海が唐から饂飩を四国に伝えて讃岐うどんが誕生したという伝説もある。
------------------
さて、複雑系(複合系)の分野では、「パイこね変換」(馬蹄形写像)という言葉があります。
( http://www.ringolab.com/note/daiya/archives/001604.html とか、 http://www.a-phys.eng.osaka-cu.ac.jp/suri-g/phys8.html の真ん中あたりとか)
パイ生地の様なものに①何か絵を描いて、②それを伸ばして折りたたんで、③(以下②を繰り返し)すると、
→最初の絵が、予想もつかない複雑なものになってしまう、という。
トランプを切るのにも似ている。配列がばらばらになる。ルービックキューブを適当に回すのにも。
------------------
カオスを生ずる言葉として、西洋では小麦粉をこねる操作として一般的な、「パイこね」変換と称されていますが、日本でも、うどんを作るときに、小麦粉をこねて伸ばして折り畳んでいく操作、この「うどん」が「カオス(混沌)」から来ているのが、面白いですね。
------------------
うどん
http://ja.wikipedia.org/wiki/%E3%83%95%E3%82%A1%E3%82%A4%E3%83%AB:Kakeudon.jpg
と、
混沌とした様子
http://www.flickr.com/photos/36761543@N02/4385051308/?edited=1
が、なんとなく似ていて面白いですね。
Δ電卓法
①
目の前の「数式」に、適当な数値(さいころを降って出た数)を、ぽつぽつと入れて、電卓でぽつぽつと計算する。
すると、なんの苦労もなく、結果が出る。
②
「①を繰り返す。」同じように、別の数値を入れて、電卓でぽつぽつと計算する。答えが出る。
①→①→・・・を繰り返す。計算結果(「Y=aX+b」的な式での、式の左辺)の数値が、3つ4つ、出てくる。
この数値を紙に書く。(野帳とかポストイットとかの、手の平以下程度のサイズでいいと思う。)
これをグラフ用紙にプロットする。手書きのグラフ用紙(軸に目盛りを適当に描いたもの)でもいいし、野帳のような方眼紙でもいい。
横軸(x軸)を何か適当な変数にして、縦軸(y軸)は、式の左辺とする。
点を3、4つほどプロットする。その点の間の空間を見て、直線か曲線かでつなぐと・・・
式の言いたいことが、イメージで分かる。
逆に、変数にどんな数値がはいったら、Yはどんな数値になるのかな、という傾向が、イメージで分かる。
「どんな数値がはいるとどんな結果が出るのか」、これは、数式を手作業で理解すること、道具として使うこと、パソコンのプログラムに置き換えること。
数式を、連続ではなく、離散(粒のつながり)として理解するのに似ている。
式を見て理解することは、ものすごく大変なことだけれども、手と紙と電卓を使うと、それ以上の領域に達することが出来る。
その理由は、頭のメモリが7個しかないから。
ちなみに、数式ではなく、表の様な数値や物事の羅列の暗記については、ボナ植木が、
①憶えたい項目に、1,2,3・・・という順番を付けて、
②例えば通勤経路などの10地点を決めて、
③項目と地点番号を対応させるストーリーを作る、
という、暗記方法を述べている。
2010年3月12日金曜日
言葉
(引用)
代名詞(だいめいし)とは、名詞ま たは名詞句の代わり に用いられる語であ る。通常は名詞とは異なる品詞と見なすが、名詞の一種とされることもある。
----------------------
括弧でくくる
----------------------
(引用)
1.再帰代名詞とは?
再帰代名詞とは、「〜自身」を意味する語のことです。
単数=〜self 複数=〜selves
http://choidebu.com/bunpou/saikidaimeishi.htm#1
----------------------
合わせ鏡
----------------------
(引用)
人間言語は必ず回帰性を持つ。 言語以外には回帰性を持つ人間の能力はない。 人間以外の動物は回帰性を持たない。
http://ocw.kyoto-u.ac.jp/faculty-of-integrated-human-studies-jp/06/pdf/11.pdf
----------------------
{再帰性・回帰性}とは、{回転・角運動・回っているコマ}のことではないか
----------------------
2010年3月10日水曜日
2010年3月9日火曜日
2010年3月8日月曜日
2010年3月7日日曜日
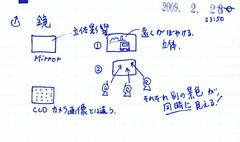
型をとる
そのとき、ひもが、ぐぐぐーっと立体的に{蓑・枠}を構成する。そして、この枠の中で、タンパク質が合成される。
これは、DNAの一部が、「自動的」に集合するのではない。そんな偶然が怒るわけがない。
ふらふらとよってきたタンパク質1分子に、くっつくようにして、DNAが、くちゃくちゃっと、まとまる。
そして、そのまとまりから、タンパク質1分子が、ぽろっと抜けて、開いた穴に、別の、アミノ酸が集合してきて、同じタンパク質1分子を、つくる。
合わせ鏡の関係。
石膏で、型を取って、複製するのと同じ。
最初に、複製したい、「対象物」がある。
それを、石膏で、かたどる。
石膏を、形が崩れないように、ばらす。
そして、真ん中の「対象物」を取り除く。
石膏を、元に戻す。そして、その穴の中に、対象物の原料を、入れる。
その中で、原料が固まって、対象物が複製される。
------------------
DNAが、そんな感じで、タンパク質分子を合成しているなら、そんなに、きっちりかっきり、していなくてもいいのではないか。
「アデニン・グアニン・シトシン・チミン」の、4つが、やってきたタンパク質1分子に対して、ちょうど、くちゃくちゃっとまとまるとうな、様々な配列をしていれば。
すなわち、DNAは、3次元的に、くちゃくちゃっとする、ということは、その1次元配列は、緻密に計算された物ではなくて、タンパク質に応じてなんかいいように、適当にならんでいる、だけでは。
ということは、DNAそのものには、やはり、{意志・心}は、無いのではないか。
考えてみたら、当たり前で、「アデニン・グアニン・シトシン・チミン」だけの4つを、並べて、意志や心ができるはずはない。
その辺の糸に意志や心がないように。
(逆に、ある「糸切れ」が、その構成分子の配列により、予想もできない{複雑な・予想もできない}「振る舞い」(周期とカオスの間の振る舞い)や「自己複製」を行うならば、その「糸切れ」は生き物であったり、{意志・心(?)}を持っているといえるのでは。)
DNAは、タンパク質に対応する石膏、というだけ。
「心」は、石膏での複製の場合は、複製される前の、例えば「彫刻」をつくった人の{心・気持ち}である。
石膏でもなければ、複製された彫刻でもない。
DNAにより複製される「生き物」の場合も、その心は、DNA(ひも)にあるのでもなく、タンパク質にあるのでもない。
タンパク質の集合体の中で生じる、合わせ鏡の「像」が、心である。
------------------
ダンスやラジオ体操の順番、空手や太極拳の型、合気道の関節技など、それを繰り返し繰り返し行う。
すると、体が、それを覚えて、頭で考えなくてもできるようになる。
「体が、覚える」と書くと、すごく神秘的というか、不思議な感じがするけれども、そんなものとは違って、実際には、やっている本人の体の体感、ぱっとある{動作・形}をとるとき、手や足の力の入れ具合、その感じ、という程度。
ボールを投げるとき、投げる人は、全身や手、脚を、一瞬で、心の中の体感で、その動作をする。ダンスや武道の場合も、体の中の体感。それを、一つの「ぱんっ」と手をたたいたときの瞬間に、全部一緒に「ぱんっ」とあわせるだけ。ボールを「ぱんっ」と投げるのと、変わらない。
「その形になろう」として外観的にやっているわけではなくて、内部の感覚で、「ぱんっ」とやっているだけ。
それで、ある一定以上やった物は、10年たっても忘れない。技の名前も順番も、すっかり忘れて、動作だけを、体が覚えている。
型でも、試合用に、とか、一定以上やった物は、一生、忘れることは無い。しかし、少ない回数しかやっていない物は、わすれている。関節技も同じ。ある一定以上の回数で、回路ができるみたい。
それは、自転車の乗り方や、キーボードのブラインドタッチ、日本や外国の言語を覚えること、かけ算の九九、すべて同じで、回数があるみたい。
回路形成(閾値)=(体感・内部の感覚)×(回数)
2010年3月6日土曜日
2010年3月2日火曜日
3-5 物理_02
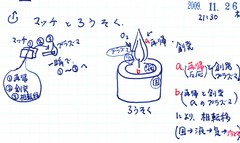
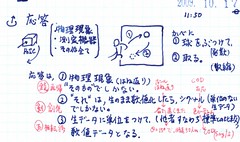
応答。
粒のぶつかりあいは、複合系(複雑系)の始まりです。
測定機器でのぶつかりを考えます。何かものを見るとき、測定機器では、{対象物・目的物・観察の対象}に何かをぶつけて、その反応を見ます。
例えば、顕微鏡では、光を当てて、反射する光を見ます。クロマトグラフでは、紙や粒と目的物がぶつかって、出てきた変化を見ます。
壁に①球をぶつけて、②それをとるのと、同じです。
壁に球をぶつけると、あらゆる方向に跳ね返る可能性が生じます(発散)。これを受け取るとき、あらゆる可能性を経て、1カ所でキャッチします(収束)。
①{物理現象・はね返り}「そのもの」でしかない。
②「それ」は、生のまま数値化したら、{シグナル・信号・単位のない生の数値}でしかない。
③{シグナル・生の数値}に単位を付けて、数値データとなる。{他者・標準・モノサシ}との比較ができる。
測定機器で目に見えないもの(温度、スピード、ある物質の濃度等)を測定する場合。一番簡単な、棒の温度計でお湯の温度を測る場合。
①お湯に温度計をつけると、中の赤い液(アルコール)が膨張します。この「膨張」は、ただの「膨張」で、これだけだと温度とは関係ありません。
②膨張した長さを測ります。3mm伸びました。この「3」という数字は、温度と関係のない「長さ」です。
③温度計の赤い部分の「長さ」と、「温度」との関係を測っておきます。
10cmのとき20℃、20cmのとき40℃、30cmのとき60℃でした。
今回のお湯では、25cmでした。このとき、お湯の温度は、先の関係から、50℃であることが分ります。
この①から③の、一連の流れの中に、情報の質的な変化、「別の概念(物理現象から、長さ、温度)への意味づけの発現」が見られます。
温度計をお湯につけたときのアルコールの反応、温度のアルコールへの「はね返り」(温度計から見ると、お湯に入って、逆にお湯からのフィードバックを受けた)が生じ、その変化を測ることで「長さ」という数値が得られ、その数値に温度(ここでは50℃)という意味づけがなされた。
測定機器では物理現象を数値化するという、質的な変化を、使用者の目的により生じています。
粒のぶつかりは、測定器の中だけではなく、自然の中、外でも海でも、情報の世界、例えばPoICのカード間でも、生じています。
2010年3月1日月曜日
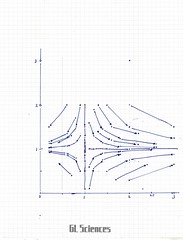
3-6 数学_05 「Nのi乗」
http://poic-kf33.blogspot.com/2009/10/blog-post_12.html
等のらせんでは、e^iθ(eのiθ乗)です。
θが変わっていく。どんどん増えていく。
e^Nθ(eのNθ乗)
と書き換えても同じです(Nが増えていく)
---------------
そして、じゃあ、eじゃなくて、Nにして、
N^i(Nのi乗)として、
Nをどんどん増やしていったらどうなるか、と思いました。
無茶な計算ですが、電卓にやらせるからいいや、と(^^;
---------------
・・・で、Nの数字をぽつぽつ選んで、どうなるのだろうか、と紙にプロットしていったら、
・・・上のカードの図のようになりました m(. .)m