y=e^(θi)について、
θ=πのとき、オイラーの公式
e^(πi)=-1
が成り立つ。
y=e^(θi)
について、θを変化させて電卓で計算してみた。
y=e^(θi)
のθを変化させると、
x軸:実数
y軸:虚数
の複素平面上で、
このθを軸にして、
x軸:y=e^(θi)の実数部分
y軸:y=e^(θi)の虚数部分
z軸:θ
の3軸の3次元座標上で、yの値を考えると、
くるくる回転がθ軸方向に引き延ばされて、らせん状となることが予想された。
また、計算してみると、オイラーの公式に似た別バージョンの等式があることが分かった。
e^(0i) -1=0
e^(π/2)i -i=0
e^(3π/2)i +i=0
e^(2πi) -1=0
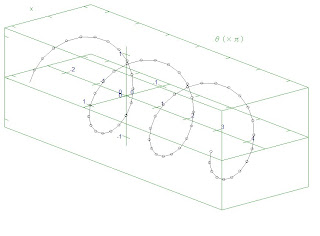
y=e^(θi)のθを変化させたときの値を、3次元空間上にプロットしてみた。
やはりらせん状になった。






0 件のコメント:
コメントを投稿