2010年5月14日金曜日
1-1-1-5-2 [創発・相転移] 構成・構造_06
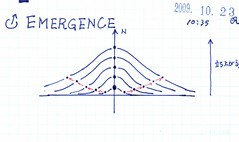
砂時計で、砂山に砂が重なっていく様子。ある一定量毎に、違う色の砂を積もらせてゆき、その断面を見ると、地層の様な模様に成っているだろう。そして、その1点、例えば、砂山の形を正規分布の釣鐘曲線(ベルカーブ)としたら、そのσ(標準偏差 http://ameblo.jp/tryangle250/image-10400932377-10325520743.html )にあたる点をつないでいったら、上方に立ち上がっていく曲線も見える。
2010年5月6日木曜日
ウルフラムの軸
に、
(引用)
-----------------------------
>ただし、この本を読んでも何が限界なのか、なぜ離散化が必要なのか、どうし
てセルオートマトンなのか、なぜ方程式でなくて離散シミュレーションなのか、
わからない。ひたすらセルオートマンによるシミュレーション(実は何について
のシミュレーションだかよくわからない)だとか、時空をネットワークグラフで
表現する方法(どうして時空をグラフ化するのか理解できない)だとか、方程式
をコンピュータシミュレーションに置き換える手法(これについては全く理解で
きない)が書いてあるばかりである。
-----------------------------
とあるけれども、これの答えは、ひょっとしたら、「離散的手続きから生まれた
マセマティカが説明できることは、離散的手続きで説明できる。他方、LISP で
はないFortran等のプログラムでは方程式を扱えるのに、数学ソフトが構築でき
ない。従ってこういう原理からは物事は説明しきれない。」ということではない
かと思った。
ウルフラムは、自身のプレゼンテーションで、マセマティカと、NKSと、検索シ
ステムのアルファの3つを軸に説明している。(アルファの構築原理は分からな
いけれども、)これは、離散的手続きから、全てのことを説明し、理解する、と
いう、ある意味シンプルな概念が、その根本にあるのではないだろうか。
(2010.5.7 追加)
Re:> http://kashino.exblog.jp/2951597/
という見方は、ひょっとしたら表面的な見方かもしれない。というのは、離散や、セルオートマトンは、表面的なもので、その奥には、「”再帰的手続き”をもとにして、物事を根底から見直す」というのがある。
そして方程式による教科書的見方は、マセマティカの範疇にあり、ウルフラムの手中にあるものであるが、これを壊してまで、マセマティカのさらに根底の原理から、科学の見方を再構築する、そしてそれは、いわゆる複雑系が扱う、「物理学や生物学が取り残した複雑な分野(相互作用、気象、生態系など)」だけではなく、「物理学や生物学そのもの(!)」でさえ、再構築する、という、構造的な意味があるのではないだろうか。
2010年5月5日水曜日
1-1-1-5-2 [創発・相転移] 構成・構造_05
カードの蓄積はまた、②脳の情報の流れにも似ている。時系列で記憶がたまってゆき、それを元に発想が生ずる。
①時間が流れ、歴史(結果)がたまってゆく。
②情報が流れ、記憶(記録)がたまってゆく。
たまるにつれて、その全体の形が滑らかになって行く。砂時計を落ちる砂粒、落ちた砂粒が数粒の時は形もない、数十粒では盛り上がりができ、数百、数千で釣り鐘の形が現われる様に。
蓄積の様子のイメージを数学の記号で表すと、砂粒の数が①少ないときは、Σ□、砂粒の数が②多くなると、∫□ 。(※ここで□は粒やカードを表す)。
1-1-1-5-2 [創発・相転移] 構成・構造_04
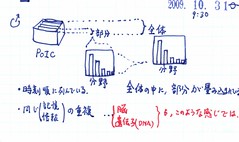
一方、その一部の塊を取り出した場合にもまた、複数の分野が混在している。部分に全体の構造が畳み込まれた、フラクタルな構造の様に、一本調子でなく、ジップの法則つまりf分の1に、自分の興味ある分野のカードがゆらいで存在している(極端なものほど少ない)ので、パラパラと繰って見たとき、心地よいのではと思います。
1-1-1-5-2 [創発・相転移] 構成・構造_03
PoICで、まず最初に①ドックにカードをためていく段階では、そこに情報のレベルでの形や構造(本の「目次」の様なもの)はありません。次に②カードがたまってゆくと、ドックの容量制限から来る精神的ストレスがたまり、また、情報カード群の塊の内部の情報エントロピーもまた、増大していきます。そこで、 ③主要なカードをごっそり抜き出して、「再生産」します。ここでは、(1)分類(グループ化)と、(2)順番を決める(順列化)の2つのことを行います。
グループ化(分類)も、順列化も、単純作業の繰り返しです。グループ化は、トランプの様に、カードの束から
①1枚目のカード[カード1]を取る。
②次のカード[カード2]を取る。
③[カード2]が[カード1]と同じグループか?
YES→[カード1]の上に置く。
NO→[カード1]の隣に置く。
④次のカードを1枚取る。→(③の作業を繰り返す)。
次に順列化。一つのグループから、
①1枚目のカード[カード1]を取る。
②次のカード[カード2]を取る。
③[カード2]は[カード1]の後か?
YES→[カード1]の後ろに置く。
NO→[カード1]の前に置く。
④次のカードを1枚取る。→(③の作業を繰り返す)。
この繰り返し作業の結果、ドックの中のカード群を、「塊・かたまり」としてみるとが出来る。個人的には、初めてごっそり再生産用にカードを取り出したとき、1年間多岐に渡るカードを投げ入れていたつもりが、大きく3(~4)個の塊に分けられることを見て、驚きました。
塊の大きさは当然ですが差があり(内容の分布は均一ではない)、サイコロを多く振れば振るほど1の目が6分の1の回数に近づく(大数の法則)ようなものとはまた違う、不均一化に向かう「見えない働き」があるのかな、と思いました。
2010年5月2日日曜日
1-1-1-5-2 [創発・相転移] 構成・構造_02
以下はPoICを始めて11ヶ月程経ったときに思った、単なる個人の予想です。
人は興味があることも興味がないこともいつも均等に考えているわけではない。偏りがある。どうしてか。興味があること(アトラクター)ほど、心を引きつけるから。人の感覚(時間や、音などの刺激)はべき乗則に従う。人の興味もまた、そうなのでは。大勢の人の人気投票(Amazon.comの商品の順位と売れ行き)はロングテールの法則(Ref: ja.wikipedia.org/wiki/%E3%83%AD%E3%83%B3%E3%82%B0%E3%83%8... )に従います。
カードが1000枚まで貯まったとする。ここでカードを分類したとき、1位から4位までの分布はどのような感じになるだろうか。ロングテールの法則のようなべき乗則に従うとしたら、ジップの式(Ref: ja.wikipedia.org/wiki/%e3%82%b8%e3%83%83%e3%83%97%e3%81%a... )のようになるのではないだろうか。この式には係数がいろいろ付いていますが、それらを単純に1としたとき、
1番目に興味がある分野が全体の3分の1(34%、340枚)とすると、
2番目に興味がある分野は1位の半分(17%、170枚)、
3番目に興味がある分野は1位の3分の1(11%、110枚)、
4番目に興味がある分野は1位の4分の1(9%、90枚)、
・
・
・
こんな感じで、興味のある(心を引きつける)分野ほど多く、興味が無くなるにつれて減少してゆくのではないかな、と思いました。
1-1-1-5-2 [創発・相転移] 構成・構造_01
「時間の流れ」は、どういうイメージで表されるでしょうか。
PoICの「時空の輪」(Ref:PoICマニュアル)では、時間の流れを、「未来から現在、そして過去へ過去へと蓄積していくカードの流れ」として表されます。葉っぱのように蓄積していくカード。
ここで流れていく情報カードは、「どんな人でも、その人の持つ再帰・創発のプロセスの中から描き出されたもの」です。そして、カード群からの再生産の成果は、「どんな人でも、その人の持つ再帰・創発・相転移のプロセスから磨き出されたもの」といえます。それは、「その人が、他の人には置き換えのできない、その人のオリジナルとして、伍していける(可能性のある)もの」なのでは、と思う様になりました。