１－１－２ カード_05

１－２　カード_05
Originally uploaded by kf333

野帳からの転記先としてPCとカードを比較すると、カードの方がPCよりも転記しやすい。PCの問題は画面の解像度も幾分あるかもしれないが、むしろ入力時の姿勢ではないかと思う。
PCのキーボード入力はナイフとフォークで肉を食べる時のように、肩が張った姿勢となり、また視線は前方に行きあごが出る。一方カードへのペンによる転記は、茶碗と箸でごはんを食べる時のように、肩が落ちて、視線は下方、両手の内側になる。モバイルＰＣの画面と５×３カードの紙面が同等の大きさであったとしても入力継続時のストレスはカードの方が小さいと感じます。

１－１－２ カード_04

１－２　カード_04
Originally uploaded by kf333

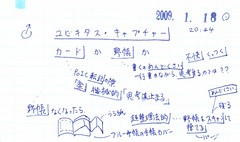
ユビキタスキャプチャーを行うのは、カードか、野帳か。
カードに直接描く場合は、転記の手間がなく楽、１項目１カードに分かれている、という特長があり、忘れないうちに（メモリが揮発する前に）急いでキャプチャーする必要があるためカードの内容（出来）はスケッチ的なものとなります。一方、野帳に記載する場合は、カードへの転記が面倒、野帳上の複数のメモは完全に分離されていない（くっついている・不快）のですが、カードへの転記はメモリの忘却を気にしなくてよいので前者と比較して清書（成書・正書・整書・聖書）的なカードが出来上がります。

１－１－２ カード_03

１－２　カード_03
Originally uploaded by kf333

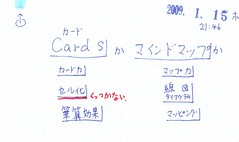
カードか、マインドマップか。
比較してそれぞれの特徴を考えてみます。
カード力は、１つ１つの項目がセル化しており、くっつかない。そろばんのような筆算効果（例．１２２＋４３７＝？を計算するときのやり方）が得られます。一方マップ力は、線図（ダイアグラム的）であり、くっついていること。またマッピング効果（面的に捉えられる）が得られます。
マインドマップは、前述の発散・収束の対比から見ると、発散的である（ただし、それが１枚のマップ（紙・カード）に、結果的に収まるので、一歩引いてみると、収束している）。カードは、１枚１項目の単位で見るならば、それぞれが収束的である（ただし、野帳に発想を描いている時や、直接カードに発想を描き出している状態は、発散的）。

１－１－２ カード_02

１－２　カード_02
Originally uploaded by kf333

発散か、収束か、につきまして。
野帳へ描く作業は拡散的（宇宙に広がるイメージ・Microsoftワードの設計・欧米的）。これに対し、カードへの転記作業は収束的（箱庭を創るイメージ・初期の一太郎の画面設計・日本的）。
ＧＴＤで１つ増えたＴＯＤＯリスト、これは、まだどうなるか分らない、発散的なイメージ（結論が出ていない）でしかない。一方ＰｏＩＣの１枚のカードは、「鏡・剣・玉」（再帰・創発・相転移）からなる１つのセット（箱庭・幕の内弁当・一匹の生き物）（結論が出ている）である。

１－１－２ カード_02

１－１－２　　カード_13
Originally uploaded by kf333

ためることについては、最初は躊躇する気持ちがありました。思いついたこと一つに１枚カードを書いていったら、あっという間にあふれてしまうのではないかと。
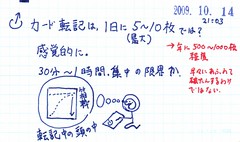
　実際には、野帳からの転記で増えるカードは、感覚的に、１日に（最大でも）５～１０枚では、と思います。３０分～１時間が、集中の限界か。あるいは、転記中の頭の枠が一杯になってしまうからでしょうか。このペースは、年に５００～１０００枚程度。ドックだと１箱で１０００枚入るので、早々にあふれて破綻するわけではないです。

１－１－２ カード_01

１－２　カード_01
Originally uploaded by kf333

野帳への記入は発散（個人のブログ）的な作業です。一方でカードへの転記は、収束的作業であり、（初めは）おっくうです（ただし増えるのは楽しい）。・・・これこそが収束的作業の特徴だと思います。
　カードへの転記は、カード(細胞)が生まれるということ。その何が楽しいのか。それは「種」であり「実」であること。
　「たった今描いた、３枚のカード」からでも、自分の好きな形をした再生産物が生まれるだろう、その可能性。それをみて、にんまりしたとしても、他の人からみたらそれが面白いのかどうかわからない、いや、むしろ面白いという保証は全くない（！）のですが、特に「まだ文章化されていない発想カード」・「記録や参照と結びついた発想」・「記録からあぶり出される今まで見えなかったパターン」、これらの文章化や形を見てみたいこと、それをみて自分が楽しい（内容は自分の好きな分野・ジャンルであるから）ことだけは確かです。

１－１－２ カード

生きている、ドックの細胞

カードの面白いところ（当初予想していなかった側面・効果）は、発想や気づき、記録が、一枚のカード（セル）として「収束」するというところ。

それは、頭の中の出来事である「再帰・創発・相転移」（鏡・剣・玉）が、やがて現われてくるであろう、しかしまだ形の見えない、大きな生き物の細胞が、１個できる、ということ。

「あっ！」を記録する。

非線形常微分方程式

非線形常微分方程式が、
（１）とても難しくて（神様でも解けない）、
（２）とても簡単（小学生でも計算できる）
な、理由。

（１）原理的に、数式処理では解けない（数式"処理"ソフトでも無理）。
（２）だから、電卓を使って、手計算で、がりがり計算するしかない。
　　（これは、小学生でも出来る単純作業の繰り返し）

で、Ｓｃｉｌａｂ等の数値"計算"ソフトは、「がりがり」（※）と、計算してく
れる。

（※）「がりがり」とは、
　�ちょこっとふやして（「足し算・引き算・かけ算・割り算」して）、
　�「足し算」、
　また、ちょこっと増やして（�に戻る）の繰り返しのこと。この「ちょこっと」
　を、もの凄く小さい数（０．０００・・・・１）とかにすると、計算回数が
１０００・・・
　回、という風に、もの凄く増える。だから、計算用紙がたくさん必要で、
　鉛筆で何枚も「がりがり」と、書かなくてはいけない、という様子。

（メモ）
　書く→（再帰・創発・相転移）→描く
　　□　　→　　○

　描く→（再帰・創発・相転移）→書く
　　○　　→　　□